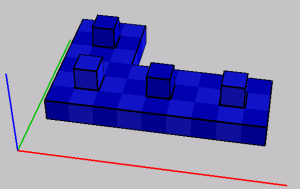
Figure: Emulation of 2-sided pieces
It is possible to emulate spacegrids different from cubes by just using cubes. This way BURRTOOLS can solve different kind of puzzles. This section will give hints on how to such things. It will not contain obvious emulation possibilities like hexagons with 6 triangles or x by y rectangles using several squares, but rather some of the more complicated possibilities. The chapter cannot be complete but rather it wants to suggest what can be done and give you some initial ideas. If you come up with a cool idea you are welcome to send it to me and I will include it here.
Generally this emulation requires using N cubes for one basic unit. This will probably result in a slowdown of the solving process, but the slowdown is not always that grave. BURRTOOLS knows how to merge voxels that are always occupied by the same piece into one, so if there is for example a puzzle that uses hexagonal pieces made out of the triangular prisms and these hexagons are always aligned on a hexagonal grid, BURRTOOLS will merge the 6 triangles together and work with the resulting shapes. This takes some time only at the initialisation phase. On the other hand, there might be many placements of pieces that fit the underlying cube to triangle grid that are not proper placements and that need to be sorted out first. This can take a long time. MAJOR CHAOS by Kevin Holmes for example has a lot of illegal placements for pieces that need to be sorted out. That takes a very long time, but once that is done the solving is actually very fast.
If you have pieces that have a top and a bottom, there are several possibilities to model that in BURRTOOLS. One possibility is to use colours. Make the piece and the result 2 layers thick. The bottom layer of both will get a special colour.
Another possibility is to add an additional layer that has voxels only in certain places as seen in the picture. The additional voxel prevents the rotation of the shape. But you have to make sure that the allowed rotations are still possible, e.g. if you place the notches in different places rotation around the z-axis is also no longer possible. An example can be seen in Figure Emul2Sided

Cubes can be cut in many different ways, to approximate shapes such as given in Figure EmulDiagCut use the 2x2x2 cube displayed there.

It is, of course, also possible to simulate diagonally cut squares this way. The squares need to be 2 layers thick.
BURRTOOLS can also handle half cubes with the Rhombic Grid. But that is more expensive because you need 24 units for a whole cubes while this emulation only needs 8 units for one cube.
Cairos are pentagons but luckily they have only 4 rotations, so it is possible to emulate them using squares. Figure EmulCairos demonstrates how that can be done.
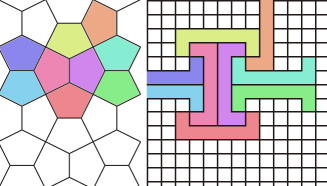
TBD
Sometimes it is possible to emulate edge matching problems by using notches and dents at the outside of the shapes.

As example let us have a look at a puzzle designed by Marcel Gillen: "Octopuz". This puzzle has pieces that are made out of 2 quatrominos. Those 2 quatrominos are connected to each other with a link and they can be turned so that in the end each piece has 4 possible shapes depending on how you rotate one halve against the other.
These shapes can be modelled using edge matching simply taking the shapes apart into their 2 halves, and colourize the touching surfaces of she 2 shapes of one piece with the same colour and a different colour for each shape.
To model such a colour edge matching problem we need to scale up by at least 3. With this scaling we are able to add dents and grooves to the basic cube so that always 2 and only those 2 cubes match independent of the rotation of one cube relative to the other. Figure Edge matching shows 5 possible such pairs of cubes. The 2 cubes in one column always are a matching pair.
There are many other shapes that can be emulated. As one example I will show 2 ways to emulate William Waites KNIT PAGODA (see Figure Pagoda1). Besides their shape the pieces have a top side and a bottom. Figure Pagoda2 shows 2 possible ways to emulate these pieces. Both shapes emulate the T-shaped piece seen on the bottom right.


It is quite easy to see how the pink shape works. It is constructed starting with a 3x3x1 square, and for each side adding a cube at the centre at the centre to represent each side that bulged outward, and removing one cube for each side that bulges inward. Finally add a cube atop the centre of the 3x3 square to make it unflippable.
The second is quite a bit more complicated to understand. Here the starting point is a 2x2 square. A cube is added or removed for the bulges just as in the other case but those cubes cannot be in the middle. They are at one side so that the cube from an outer bulge can go into a gap created by an inner bulge. The resulting shape for one unit contains 4 cubes along a zig-zag line. You can see it by looking for the lighter cubes in the cyan shape above. This way has the additional advantage of avoiding flips because when the piece is flipped over the orientation of the bulges changes and the cubes do not mesh.